Cơ sở Kỹ thuật điện (CSKTĐ) là môn học cơ sở Kỹ thuật quan trọng trong chương trình đào tạo Kỹ sư ngành Kỹ thuật điện. Nó cung cấp những cơ sở lý luận chung nhất, những phương pháp cơ bản để tính toán, giải thích các hiện tượng điện từ của thiết bị điện. Bài viết tổng hợp những khái niệm cơ bản nhất về mô hình mạch mà lý thuyết mạch điện, mong rằng chúng sẽ giúp ích được cho các bạn trong quá trình học tập.
I. Mô hình toán học mô tả một vật thể vật lý, kỹ thuật
1. Phương pháp luận mô hình toán học
− Muốn sử dụng, điều khiển, cải tạo một vật thể vật lý kỹ thuật cần phải nhận thức, hiểu biết về tổ chức, cấu trúc, cơ chế, quy luật hoạt động của nó.
− Vật thể vật lý hoạt động trong không gian, thời gian gọi là quá trình, một vật thể vật lý có nhiều quá trình, như quá trình điện từ, cơ, nhiệt... Về nguyên tắc là vô cùng nhiều các quá trình. Vì vậy cần nhận thức hiểu biết vật thể tức là nhận thức hiểu biết các quá trình (về nguyên tắc chỉ nhận thức được một số hữu hạn các quá trình đó của vật thể).
− Quá trình mang đặc điểm, quy luật riêng của vật thể gọi là hiện tượng. Một vật thể có thể được thể hiện qua nhiều hiện tượng.
− Mỗi ngành chỉ quan tâm đến một số hiện tượng mô tả quá trình nào đó. Những hiện tượng đó gọi là những hiện tượng cơ bản, vì vậy nhận thức vật thể là nhận thức các hiện tượng cơ bản mà ta quan tâm. Để có thể sử dụng tốt các nhận thức cần được mô tả bằng các công thức toán học. Vậy biểu thức toán học mô tả nhận thức quá trình gọi là mô hình toán học của quá trình đó. Nó là cách quan niệm và hình dung bằng chủ quan của ta bằng toán học về một loại quá trình.
2. Đặc điểm của mô hình toán học
− Vì mô hình là mô tả định lượng nhận thức của con người về vật thể nên mô hình toán học có tính chủ quan. Nó là sản phẩm của tư duy con người, nó phản ánh trình độ khoa học kỹ thuật của thời đại. Nó cũng tùy thuộc vào những yêu cầu của việc vận dụng thực tiễn. Ví dụ tùy theo độ tiện dụng và độ chính xác mà quá trình điện từ trong thiết bị điện có thể miêu tả bằng hệ phương trình Macxuel hoặc phương trình Laplace hoặc hệ phương trình Kirhof (KF), các phương trình này lại có thể coi là tuyến tính hay phi tuyến...
− Bên cạnh tính chủ quan, mô hình toán học phải có tính khách quan nhất định. Nó phải phản ánh được quy luật khách quan của quá trình với độ chính xác cần thiết, cần được kinh qua kiểm nghiệm thực tiễn công tác, và phải được xây dựng đủ chặt chẽ về logic.
− Do có tính chủ quan và khách quan đó nên một loại quá trình của vật thể có thể có nhiều mô hình toán học tùy theo yêu cầu về độ chính xác. Ngược lại những quá trình khác nhau lại có thể chung những mô hình toán học.
3. Ý nghĩa của mô hình toán học
Mô hình toán học có những ý nghĩa rất quan trọng
− Về mặt nhận thức : mô hình toán học giúp ta nhận thức, hiểu biết đúng về vật thể.
− Về mặt thực tiễn công tác : mô hình là một cơ sở lý luận dùng vào việc xét, sử dụng, khống chế vật thể. − Về mặt lý luận : mô hình toán học không những là cơ sở lý luận mà còn là nội dung và đối tượng của một lý thuyết.
Ví dụ : xét quá trình điện từ của Thiết bị điện (TBĐ) có thể lập những cách mô tả toán học khác nhau làm thành nội dung cơ sở cho nhũng lý thuyết khác nhau. Ta sẽ thấy sức mạnh, độ chính xác... của lý thuyết được quyết định bởi sức mạnh, độ chính xác... của mô hình toán học. Mặt khác một nội dung nữa của lý thuyết chính là việc nghiên cứu cách vận dụng mô hình toán học để phân tích tìm thêm những hiện tượng của quá trình, sử dụng quá trình vào những mục đích thực tiễn và để khống chế, tổng hợp ra những quá trình cần thiết.
II. Cách xây dựng mô hình toán học
Từ định nghĩa mô hình toán học ta thấy phải qua các bước để xây dựng mô hình như sau :
1. Phân tích, liệt kê nhóm đủ các hiện tượng cơ bản, là những hiện tượng từ đó hợp thành ra mọi hiện tượng khác thuộc mặt ta xét.
2. Chọn và định nghĩa các biến trạng thái. Đó là những hàm hay vectơ x(r,t...) phân bố trong thời gian và không gian để đo quá trình.
Ví dụ : E(r,t), B(r,t), ..., uk(t), ik(t)...
3. Mô tả toán học cơ chế các hiện tượng cơ bản, đây chính là phương trình liên hệ giữa các biến trạng thái. Gọi là phương trình trạng thái.
4. Mô tả việc hợp thành các quá trình cụ thể, thường bằng cách kết hợp những phương trình trạng thái cơ bản trong một phương trình cân bằng hoặc nói chung một hệ phương trình trạng thái.
5. Kiểm nghiệm lại mô hình trong thực tiễn hoạt động của vật thể xét.
III. Hai mô hình toán học - Hệ thống và trường
Theo cách phân bố không, thời gian của biến trạng thái có thể xếp mô hình toán học thành hai loại :
Mô hình hệ thống (mô hình Mạch ) : Là mô hình trong đó quá trình được đo bởi hữu hạn các biến trạng thái xk(t) chỉ phân bố trong thời gian mà không phân bố trong không gian. Vì biến chỉ phụ thuộc thời gian nên tương tác các biến chỉ quan hệ nhân quả trước sau trong thời gian, đó là quan hệ trước sau, trạng thái ở t chịu ảnh hưởng của những trạng thái trước t kể cho đến một khởi đầu to nào đó. Vì không có quan hệ nhân quả trong không gian; các biến ảnh hưởng nhau tức thời, coi vận tốc truyền tương tác trong mô hình này là vô cùng lớn.
Về mặt toán học, hệ chỉ phân bố thời gian thường là hệ vi tích phân, vi sai phân hoặc đại số trong thời gian ứng với bài toán sơ kiện (điều kiện đầu).
Trong thực tế rất hay gặp những hệ thống mà quá trình ngoài dạng biến thiên theo thời gian còn gắn với một sự lưu thông (chảy, truyền đạt) các trạng thái giữa những bộ phận hệ thống.
Ví dụ : trong các thiết bị động lực có sự truyền đạt năng lượng, có các dòng điện chảy, trong hệ thống thông tin - đo lường - điều khiển hoặc hệ thống rơle có truyền đạt tín hiệu, trong các hệ thống máy tính có sự truyền đạt những con số...ta gọi những mô hình đó là mô hình mạch, một dạng khá phổ biến của mô hình hệ thống.
Đến đây có thể định nghĩa mạch điện là một hệ thiết bị điện trong đó ta xét quá trình truyền đạt biến đổi năng lượng hay tín hiệu điện từ, đo bởi một số hữu hạn biến dòng, áp, từ thông, điện tích...chỉ phân bố trong thời gian.
2. Mô hình trường : Là mô hình trong đó quá trình được đo bởi một số hữu hạn biến x(r,m,t,...) phân bố trong cả không gian và thời gian. Về mặt tương tác, ngoài quan hệ nhân quả trước sau còn thêm quan hệ trong không gian. Trạng thái ở một điểm không gian (r,m,t...) còn chịu ảnh hưởng của những trạng thái ở lân cận điểm đó, kể cho đến một bờ So nào đó.
Về mặt toán học những hệ phân bố trong không gian và thời gian được mô tả bằng những phương trình đạo hàm riêng phần trong không gian và thời gian ứng với bài toán vừa có sơ kiện vừa có biên kiện (bờ). Xét một quá trình tùy vào yêu cầu về độ chính xác mà có thể dùng mô hình trường hay mô hình mạch.
IV. Lý thuyết mạch và điều kiện mạch hóa
Các điều kiện mạch hóa là những điều kiện cần thỏa mãn để có thể xây dựng mô hình mạch mô tả quá trình.
Các điều kiện mạch hóa bao gồm:
1. Đối với quá trình xét, vật thể phải là một hệ thống theo nghĩa đã nêu.
2. Có thể định nghĩa một số hữu hạn biến trạng thái phân bố trong thời gian xk(t) để đo quá trình xét.
3. Có thể mô tả quá trình bằng một hệ hữu hạn phương trình trạng thái riêng theo thời gian.
V. Phân loại mô hình hệ thống
Căn cứ theo phép tính tác động lên biến trong hệ phương trình, xếp các mô hình hệ thống thành 4 loại chính:
1. Mô hình mạch truyền đạt: Loại này ứng với phương trình vi phân có phép tính là các phép toán tử T như phép tính đạo hàm, tích phân hoặc quan hệ hàm số. Nói chung nó là một phép làm ứng với một hàm hay vectơ x(t) với một hàm hay một vectơ y(t). biểu diễn ở hình M-1.
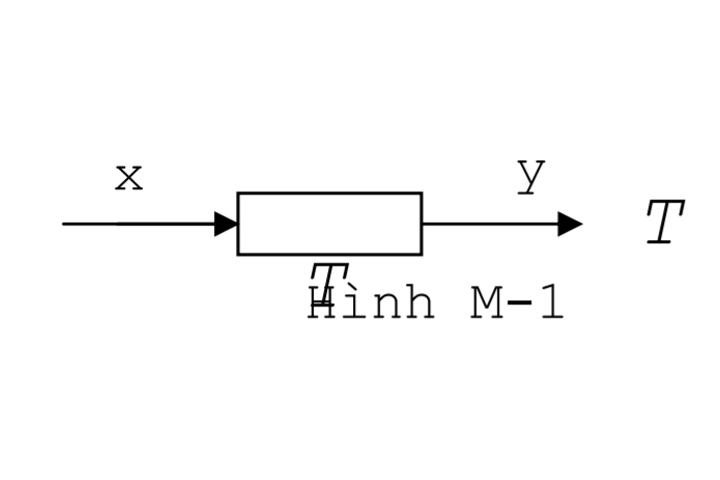
2. Mô hình mạch năng động lượng (Mô hình mạch KF): Loại này ứng với phương trình vi phân với phép toán tử T như trên nhưng đặc biệt ở đây quá trình đo bởi những cặp biến xk(t), yk(t) với nội tích xk.yk = pk là năng lượng hay động lượng thỏa mãn luật bảo toàn và liên tục. Trong hệ thống này có sự truyền đạt năng lượng giữa các bộ phận. (Có thể coi mô hình năng lượng là trường hợp riêng của mô hình truyền đạt - là mạch chỉ quan tâm đến tín hiệu).
3. Mô hình mạch lôgic: Loại này ứng với hệ phương trình đại số lôgic với phép tác động lên biến là quan hệ hàm logic L. Đó là phép làm ứng với một trong hai giá trị (0,1) của x với một trong hai giá trị (0,1) của y. Biểu diễn ở hình M-2.
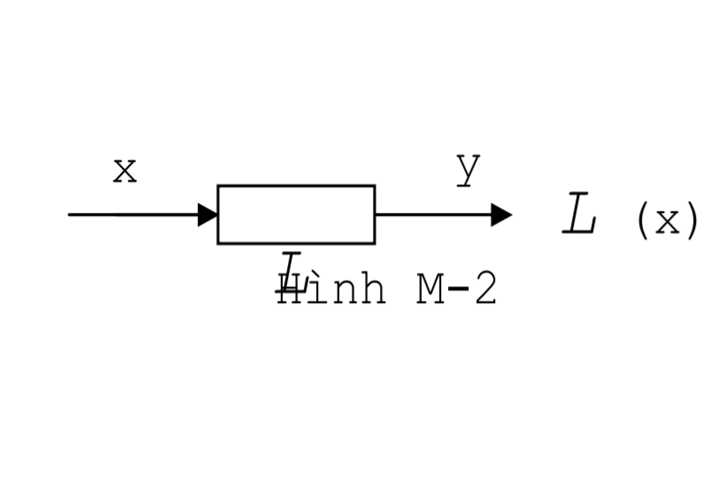
4. Mô hình mạng vận trù: Loại này ứng với hệ phương trình phiếm hàm có phép tác động lên biến là phép phiếm hàm F. Đó là cách làm ứng một hàm x(t) với một số a[x(t)] để đánh giá quá trình x(t). Biểu diễn bởi công thức sau:
< F, x(t) > = a[x(t)].
VI. Mô tả quá trình thời gian (mô hình mạch) bằng sơ đồ hình học, gọi là những graph
Vì quá trình không phụ thuộc không gian nên có thể dùng những hình vẽ trong không gian để biểu diễn mạch.
Vì quá trình chỉ phụ thuộc thời gian, quá trình có v = ∞ là quá trình tức thời nên hình thành các vùng năng lượng - nên TBĐ được coi là sự chắp nối các vùng năng lượng với nhau. Mỗi vùng năng lượng là một phần tử thì mạch điện là sự chắp nối các phần tử thành sơ đồ nghiệm đúng hệ phương trình mạch. Vậy mạch điện có kết cấu khung gồm những phần tử lắp nối thành sơ đồ mạch.
Các yếu tố hình học của sơ đồ gồm:
1. Phần tử: Là phần của mạch mà ta không đặt vấn đề chia nhỏ thêm - nó biểu diễn một vùng năng lượng như: R, L, C, Z, Y, e, j.
2. Nhánh: Là là tập hợp các phần tử mà trên đó có cùng một dòng chảy.
3. Đỉnh (nút): Là chỗ gặp nhau của các nhánh.
4. Vòng: Là đường đi kín qua các nhánh. Hình hình học chắp nối các phần tử có định nghĩa các biến và quy luật liên hệ các biến, thì nó biểu diễn được hệ phương trình thời gian. Nó là sơ đồ mạch - đồng nhất với mô hình mạch gọi là các graph. Có nhiều loại graph như: graph năng lượng, graph tín hiệu, graph định chiều, graph không định chiều.
Ngoài ra có thể định nghĩa thêm một số yếu tố hình học khác như:
5. Cây mạch điện: Là một tập hợp nối đủ các đỉnh nhưng không tạo ra vòng kín nào. Trong một graph số cây là hữu hạn và có thể có nhiều cây khác nhau ứng với một graph. Mỗi nhánh của cây gọi là một cành. Nếu mạch có m nhánh, d đỉnh thì số cành là k1 = d-1(nếu là graph đơn liên), k1= d-l (nếu là graph đa liên và l là số liên) Graph là đơn liên nếu mọi đỉnh đều liên thông với nhau.
6. Bù cây mạch điện: Là tập nhánh của graph ghép nối với cây tương ứng để hợp thành graph đã cho. Nhánh của bù cây gọi là bù cành. Số bù cành của một bù cây là: k2= m - k1= m -d +1 (ứng với graph đơn liên), k2 = m - d + l ứng với graph đa liên. Số cành và số bù cành chỉ tùy thuộc vào d, m, l của graph, tức là tùy thuộc vào cấu trúc mạch. Ta sẽ thấy chúng liên quan chặt chẽ với số biến và số phương trình độc lập viết theo luật KF.
Từ định nghĩa cây, bù cây ta thấy:
− Các áp cành trên một cây làm thành một tập đủ áp nhánh độc lập. Hay số áp nhánh độc lập đúng bằng số cành k1 = d-1.
− Các dòng bù cành trên một bù cây làm thành một tập đủ dòng nhánh độc lập. Hay số dòng nhánh độc lập chính bằng số bù cành k2 = m-d+1. Ví dụ ở hình vẽ M-3.1 là graph với m = 8, d = 5, l = 1, M-3.2 là cây, M-3.3 là bù cây:
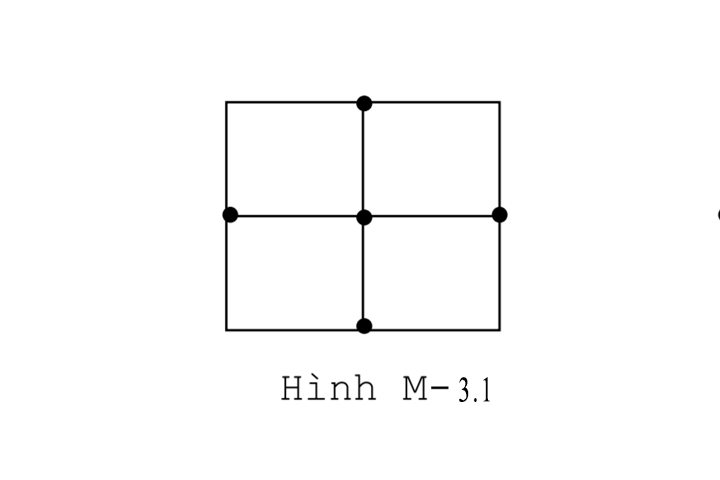
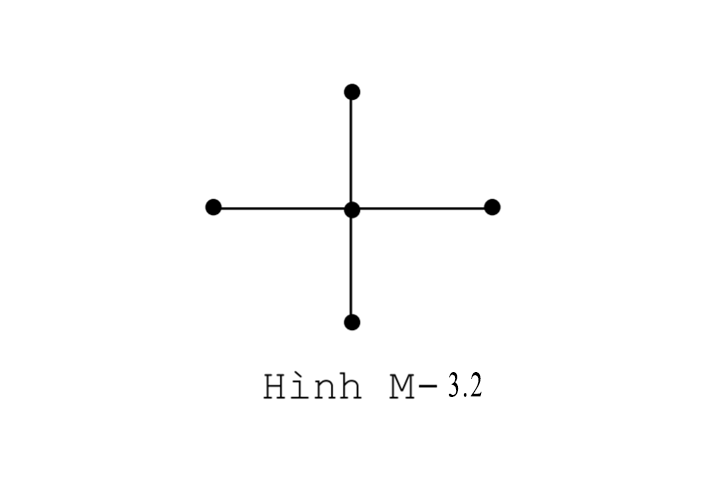
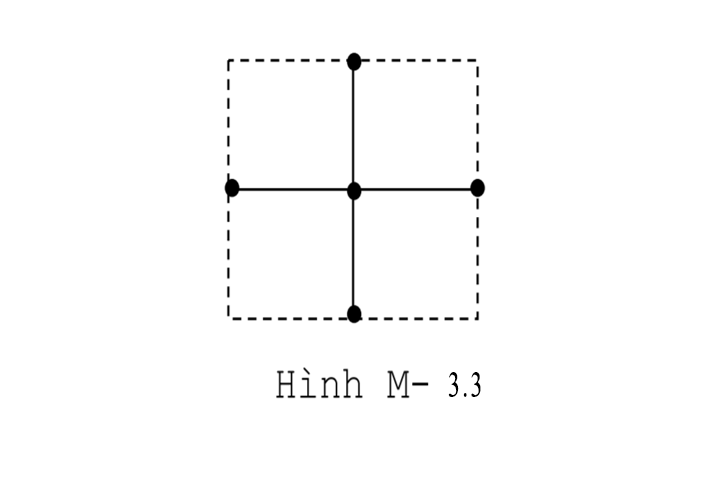
VII. Hai bài toán của mạch điện
Có hai dạng bài toán: bài toán phân tích và bài toán tổng hợp.
1. Bài toán phân tích mạch điện: Là bài toán cho biết sơ đồ (kết cấu, thông số), biết kích thích tác động vào mạch (thường là nguồn) cần phải xác định áp, dòng, công suất ở một nhánh nào đó (thường gọi là đáp ứng).
2. Bài toán tổng hợp mạch điện: Đây là bài toán đã biết kích thích (coi là nguồn phát), và cũng đã biết đáp ứng ở một nhánh nào đó (thường là một yêu cầu sử dụng nào đó). Cần phải xác định cấu trúc và thông số của mạch để thỏa mãn quan hệ giữa kích thích và đáp ứng đã biết ở trên.
VIII. Phân loại mạch điện
Có hai cách phân loại, theo tính chất của mạch điện chia làm hai loại mạch điện:
1. Mạch điện tuyến tín: Gồm tất cả các phần tử trong mạch là tuyến tính, ứng với hệ phương trình vi phân tuyến tính (trường hợp đặc biệt là hệ phương trình đại số tuyến tính).
2. Mạch điện phi tuyến: Là mạch điện có chứa phần tử phi tuyến, ứng với hệ phương trình vi phân (hay đại số) phi tuyến.
Theo chế độ làm việc của mạch điện ta chia ra các loại:
1. Mạch điện xác lập: Là mạch điện làm việc bình thường, ổn định.
2. Mạch điện quá độ: Là mạch điện chưa đạt đến trạng thái làm việc xác lập ổn định mà đang chuyển từ trạng thái này sang trạng thái khác.
Tìm hiểu các bài viết khác tại Linh Kiện Điện Tử 3M
>> Tổng hợp những mạch điện tử cơ bản
>> Điện tử căn bản- Các linh kiện- mạch điện cơ bản








